Proste całkowanie

Każdy student uczelni technicznych zapewne zapoznał się z cudownym aparatem matematycznym jakim są całki i różniczki.
Powinien również bardzo łatwo napisać algorytm na liczenie całki oznaczonej. W praktyce jednak wiadomo jak to bywa. Poniższy artykuł przybliży laikowi całki. Algorytm jest dla bardzo początkujących :).

Najpierw przypomnę czym jest całka. Chodzi mi jedynie o łopatologiczne wytłumaczenie na potrzeby artykułu.
Całka po prostu to operacja matematyczna licząca pole pod dowolną krzywą, jeżeli mamy wzór wykreślający ją.
Przykładowa notacja całki oznaczonej (będę ją stosować w całym artykule):

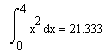
Zapis ten oznacza, że pole pod krzywą x^2 z przedziału od 0 do 4 wynosi 21.333.

W programowaniu jest wiele algorytmów, dzięki którym można to osiągnąć. Od najprostszych numerycznych aż po potężne symboliczne. Moja wiedza niestety ogranicza się na tych pierwszych :).

Problem z liczeniem pola pod krzywą polega na tym, że nie znamy wzoru, aby go policzyć. Natomiast doskonale znamy wzór na pole prostokąta.
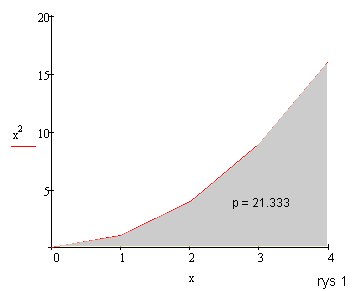
Algorytm polega na tym, że dzielimy figurę utworzoną przez krzywą na bardzo małe prostokąciki, a następnie dodajemy ich pola do siebie. Rozjaśni to rysunek 2:

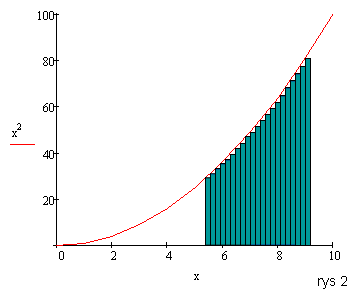
Widzimy, że prostokąty nie wypełniają dokładnie przestrzeni pod krzywą. Można też zauważyć, że im węższy prostokąt, tym dokładniejsze nasze obliczenia. Całka w praktyce to podzielenie tej powierzchni na nieskończenie wąskie prostokąty. Niestety my musimy się zadowolić jedynie bardzo małymi wartościami.

Skoro już wszystko wiemy, to możemy się zająć pisaniem programu.

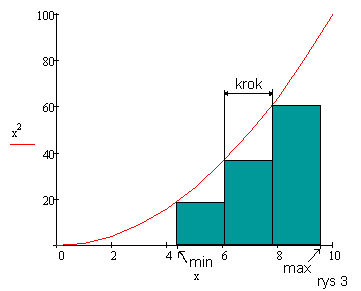
Min i max będą przedziałami, a krok szerokością prostokąta.
Kod funkcji liczącej całkę:

function Calka(Funkcja: TMathFunction; Min, Max, Krok: Extended): Extended;
var
  X: Extended;
begin
  X := Min; // Przypisujemy początkową wartość do argumentu
  Result := 0;
  while X < Max do begin // Kończymy pętle jak dojedziemy do końca przedziału
    Result := Result + Krok * Funkcja(X); // Krok * Funkcja(X) to pole naszego prostokąta
    X := X + Krok; // Zwiększamy argument o szerokość prostokąta
  end;
end;

Funkcja to wskaźnik do funkcji matematycznej. Musimy zadeklarować typ danych:

type TMathFunction = function(const X: Extended): Extended;

W praktyce wygląda to tak (na formie umieszczamy przycisk):

function Xkwadrat(const X: Extended): Extended;
begin
  Result := X * X;
end;

procedure TForm1.Button1Click(Sender: TObject);
var
  wynik: Extended;
begin
  wynik := Calka(Xkwadrat, 0, 4, 0.00001);
  ShowMessage(Format('%.3f', [wynik]));  // Wyświetlamy wynik z dokładnościa do 3 miejsc po przecinku
end;

Powinno nam wyskoczyć okienko z poprawną wartością, tj. 21.333.